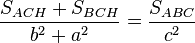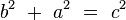Los Jonas Brothers se pelean (teoría de juegos)
Un trielo es similar a un duelo, con la diferencia de que hay tres participantes en lugar de dos. Una mañana, Kevin, Joe y Nick (sí, los Jonas Brothers) deciden acabar un conflicto (quién ha cogido mi anillo de castidad?, has sido tú Nick?, No yo no he sido, Eres idiota, solucionemos esto como hombres que somos...) participando en un trielo con pistolas hasta que sólo quede uno de ellos. Kevin es el peor tirador porque su promedio de aciertos es de uno de cada tres disparos. Joe es algo mejor porque su media está en dos aciertos de cada tres intentos. Nick es el mejor, siempre hace diana. Para hacer el trielo mñas justo dejan que Kevin dispare primero, luego podría tirar Joe (si sigue vivo) y detrás de él Nick (si no está muerto para entonces), y vuelta a empezar hasta que sólo quede uno de ellos. La duda es: ¿hacia dónde debería derigir Kevin su primer tiro?
Solución
Examinemos sus opciones. Primero Kevin podría a puntar a Joe. Si acierta, el siguiente disparo lo efectuará Nick. A Nick sólo le queda un oponente, Kevin, y ya que Nick nunca falla ningún tiro, Kevin está muerto.
Una opción mejor es apuntar a Nick. Si tiene éxito entonces el siguiente disparo corresponde a Joe, que sólo da en el blanco 2 de cada 3 veces, por lo que existe la posibilidad de que Kevin sobreviva para disparar otra vez él a Joe y quizás, ganar el trielo.
Parece que la segunda opción es la que debería seguir Kevin. Sin embargo existe una tercera opción aún mejor. Kevin podría apuntar al aire. el próximo disparo le corresponde a Joe, y él apuntará a Nick, puesto que es el oponente más peligroso. Si Nick sobrevive apuntará a Joe, puesto que es su más peligroso oponente. Apuntando al aire Kevin está permitiendo que Joe elimine a Nick o viceversa.
Ésta es la mejor estrategia de Kevin. al final, Joe o Nick morirán y entonces Kevin disparará al superviviente. evin ha manipulado la situación de manera que, en lugar de tener el primer disparo en un trielo, tiene el primer disparo en un duelo.

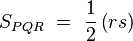
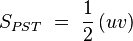
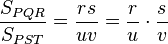
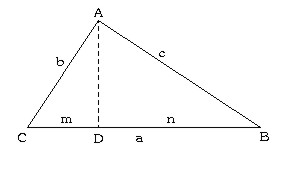
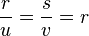 la razón de semejanza, está claro que:
la razón de semejanza, está claro que: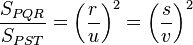

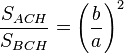
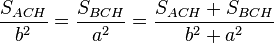 (I)
(I) 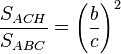
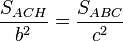
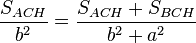 , así que:
, así que: