4ª demostación del Teorema de Pitágoras.
Pitágoras también pudo haber demostrado el teorema basándose en la relación entre las superficies de figuras semejantes.
Los triángulos PQR y PST son semejantes, de manera que:

(r/u) = (s/v) = r’
siendo r’ la razón de semejanza entre dichos triángulos. Si ahora buscamos la relación entre sus superficies:
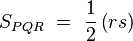
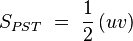
obtenemos después de simplificar que:
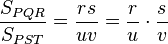
pero siendo 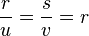 la razón de semejanza, está claro que:
la razón de semejanza, está claro que:
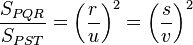
Es decir, "la relación entre las superficies de dos figuras semejantes es igual al cuadrado de la razón de semejanza".
Aplicando ese principio a los triángulos rectángulos semejantes ACH y BCH tenemos que:

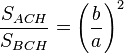
que de acuerdo con las propiedades de las proporciones nos da:
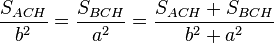 (I)
(I)
y por la semejanza entre los triángulos ACH y ABC resulta que:
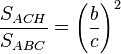
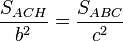
pero según (I) 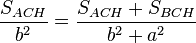 , así que:
, así que:
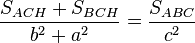
y por lo tanto:
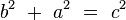 Q.E.D.
Q.E.D.
0 comentarios