6ª demostración del Teorema de Pitágoras

   Para esta demostración hemos de utilizar el concepto de potencia de un punto, muy utilizado en dibujo técnico. Explicamos el concepto de potencia de un punto.

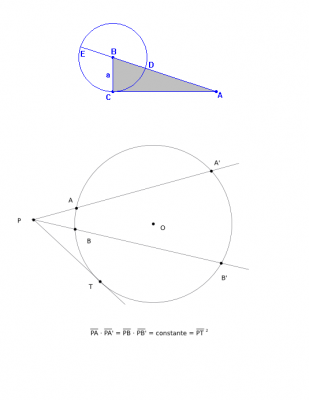
   Sean una circunferecia C y un punto fijo P (que en este caso, para no complicar la cosa, será exterior a la circunferencia), la potencia del punto P respecto a C es el producto de las distancias a cualquier par de puntos de la circunferencia alineados con P. Para entender mejor esto, vamos a demostrarlo on el Teorema de Tales, que postula que dadas dos rectas secantes seccionadas por rectas paraleleas, los segmentos entre rectas son proporcionales. Entonces podemos expresar según la imagen de abajo:

           PA/PB = PA’/PB’   

           ó PA/PA’ = PB/PB’

           ó PA/PB’ = PB/PA’

   Con lo que podemos escribirlo así:

          PA · PA’ = PB · PB’

  Y nos llevamos esta relación al dibujo de arriba, podemos escribir:

             AD · AE =  AC²

    Como BE = BC = BD= a y AD = c - a; AE = c + a; AC = b entonces sustitutímos:

   (c - a)·(c + a) = b²

   Según las igualdades notables aquñi demostradas, operamos:

   c ² - a² = b²

   Que podemos ponerlo así:

      c² = b² + a²               Quod erat demostrandum (Q.E.D.)