Demuestra la siguiente igualdad:

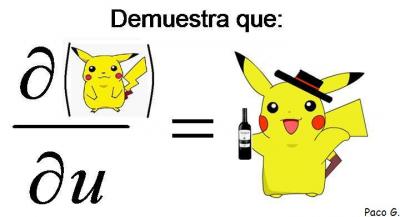
   Pues sí, pikachu está metido también en el mundo de las matemáticas. Para que veais la gracia del asunto, os pondré la solución hoy mismo.

      SOLUCIÓN:

   La expresión de la derecha se puede escribir de la siguiente manera:

                                    ∂[ π · K · ch(u) ] 

                               ------------------------------

                                            ∂(u)

   Donde K y π son constantes, ch es una forma de expresar el coseno hiperbólico (en el que en vez de hacerse con una circunferencia, se hace con una hipérbola) y u es la variable con respecto a la que hemos de derivar parcialemnte (∂ significa derivada parcial).

   Si recordamos la definición de la derivada y las reglas de derivación, pasaría lo siguiente. K y π, al ser constantes que multiplican a una variable [ch(u)], no les pasan nada. Con respecto a ch(u), calculamos su derivada. La derivada del coseno hiperbólico es el seno hiperbólico, que se representa como sinh o sh(u). Con todos estos datos, podemos sustitutír y nos queda lo siguiente:

                           ∂[ π · K · ch(u) ] 

                               ------------------------------   =   π · K · sh(u)

                                            ∂(u)

    Por tanto, la derivada parcial de pikachu es π · K · sh(u), que se puede leer como pikashu, o sea, el pikachu andaluz. Por cierto, el número pi es tan importante que pikachu no deja de recordarnoslo todos los días, XD.

   Obtenido de gaussianos.com