5ª demostración del Teorema de Pitágoras (de 367 conocidas)

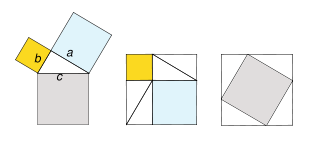
Partiendo de la configuración inicial, con el triángulo rectángulo de lados a, b, c, y los cuadrados correspondientes a catetos e hipotenusa –izquierda-, se construyen dos cuadrados iguales:

• Uno de ellos –centro- está formado por los cuadrados de los catetos, más cuatro triángulos rectángulos iguales al triángulo inicial.
• El otro cuadrado –derecha- lo conforman los mismos cuatro triángulos, y el cuadrado de la hipotenusa.

Si a cada uno de estos cuadrados les quitamos los triángulos, evidentemente el área del cuadrado gris (c²) equivale a la de los cuadrados amarillo y azul (b² + a²), habiéndose demostrado el teorema de Pitágoras.

Quizá esta forma no quede muy clara, o incluso inductiva, por lo que recurriremos a un razonamiento deductivo. Fijémonos pues en la figura del centro. Si el valor del lado del cuadrado amarillo es a y el lado del cuadrado azul es b, el área del cuadrado total es, según la Igualdad Notable I que demostramos anteriormente de forma gráfica:

   (a + b)²  = a² + b² + 2 · a · b  

Y si nos fijamos en la figura de la izquierda, el área total será el área de los cuadro cuadrados más la del cuadrado gris de lado c, que se puede expresar de esta manera:

   (a + b)²  = c² + 4 (a · b)/2

Donde (a · b)/2 es el área de uno de los triángulos. Si igualamos las expresiones nos queda:

   a² + b² + 2 · a · b = c² + 4 (a · b)/2

   a² + b² = c²

                                                                                                                                     ^Q.E.D