2ª demostración del Teorema de Pitágoras
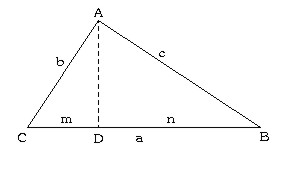
Esta demostación se basa en el teorema del cateto.
De un triángulo rectángulo ABC, trazamos su altura desde su ángulo recto, obteniéndo así dos triángulos semejantes ACD y ABD. Dada su semejanza, podemos esrtablecer las siguientes relaciones:
En el triángulo ABC a es a b como en el triángulo ACD b es a m. Que se escribiría una cosa tal que así:
(a/b) = (b/m)
Lo que es igual a: b2 = a · m (1)
En el triángulo ABC a es a c como en el triángulo ABD c es a n. Que se escribiría una cosa tal que así:
(a/c) = (c/n)
Lo que es igual a: c2 = a · n (2)
Según las ecuaciones 1 y 2, si las sumamos queda:
b2 + c2 = a · n + a · m
b2 + c2 = a ( n + m )
b2 + c2 = a2
Q.E.D
(quod erat demonstrandum)
0 comentarios