9ª demostración del Teorema de Pitágoras

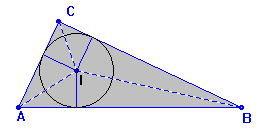
   Calculamos el área del triangulo ABC de dos formas diferentes.

   Una forma posible es sabiendo que el área de un triangulo es igual al semiperímetro por el radio del circulo inscrito o lo que es lo mismo, la suma de las áreas de los tres triángulos que se forman, siendo la base el lado y la altura el radio. s es el semiperímetro y r es el radio de la circunferencia inscrita.

     Area = s · r = (a + b + c)/2 · r = (a · r)/2 + (b · r)/2 + (c · r)/2

   De la figura se tiene que la hipotenusa c = (a - r) + (b - r) (comprobémoslo como si usásemos un compás, trasladando esa medida a la hipotenusa. Nota importante: el segmento que queda desde el punto de cotre del radio con los catetos a y b hasta el ángulo rectangulo tiene la misma medida que el radio) de donde r = s - c.

     Area = s · r = s · (s - c)

   Sabiendo además que el área del triángulo es también el semiproducto de la base por la altura:

         Área = Bas · alt /2 = a · b / 2.

Igualando las expresiones anteriores y sabiendo que s = (a + b + c)/2 por sustituir lo anterior:

      s · (s - c) = a · b/2

     (a + b + c)/2 · (a + b - c)/2 = ab /2 

     (a + b + c) · (a + b - c) = 2ab

     (a + b)² - c² = 2ab 

      a² + b ² + 2ab - c² = 2ab;

      a² + b² = c²              Quot erat demostrandum (Q.E.D.)