10ª demostración del Teorema de Pitágoras o demostración de Einstein

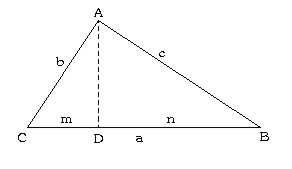
   En el triángulo original, de lados a, b, c, trazamos una altura. Se forman así dos nuevos triángulos rectángulos. El de la izquierda o el menor tiene por hipotenusa a cuya área nombraremos por S_a,, el de la derecha o el mayor tiene por hipotenusa b, y su área será S_b y el triángulo original, con hipotenusa c, tendrá un área S_c.

   Estos tres triángulos son semejantes porque tienen ángulos iguales. En el plano euclídeo, el área de cualquier figura geométrica es proporcional al cuadrado de su dimensión lineal. Podemos escribir por tanto que:

         S_a = K · a²
         S_b = K · b²
         S_c = K · c²

   Donde K es una constante igual en las tres ecuaciones (ya que los triángulos, al ser semejantes, son la misma figura geométrica).

Además, es obvio que

        S_c = S_a + S_b

Sustituyendo aquí las ecuaciones anteriores:

       K · c² = K · b² + K · a²

       c² = a² + b²            Quot erat demostrandum (Q.E.D.)

   Se dice que cuando Einstein tenía once años, su tío Jacob le enseñó la demostración de Euclides del teorema de Pitágoras. Al pequeño Albert le pareció demasiado complicada, y pensando sobre el asunto, dio con esta prueba.