Teorema de Pitágoras (demostración sagrada número 1)
Bueno, primero explico el título. Para mí y para otros pocos más hay tres demostrasiones mu sensillitas pero muy importantes (como las tres manifestaciones de Dios, pues igual) que nunca está de más ver: La del teorema de pitágoras, la de la irracionalidad de √2 y la de que existen infinitos números primos. Vamos a empezar por Pitágoras:
Es famosa la frase "en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos". Existen varias formas de demostrarlo. Por lo pronto vamos a poner una, aunque ampliaremos otro día con alguna más:
Antes de empezar: el área del cuadrado se calcula elevando su lado al cuadrado. La del triángulo es (base x altura) / 2
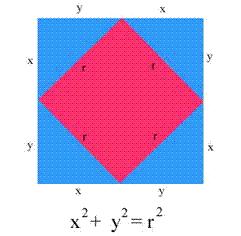
En la imagen de arriba se ven dos cuadrados: uno con lado "r", de color rosa, y otro con lado "x + y", el más grande. Al mismo tiempo observamos cuatro triángulos rectángulos, con catetos "x" e "y", e hipotenusa "r". Lo que queremos demostrara es que r2 = x2 + y2. Para ello vamos a empezar escribiendo la relación existente entre las áreas de los dos cuadrados.
(x + y)2 = área del cuadrado grande
r2= área del cuadrado rosa
(x*y) / 2 = área del triángulo rectángulo
El área del cuadrado grande es igual a la del cuadrado rosa más cuatro veces el áres de uno de los triángulos. Es decir:
(x + y)2 = r2 + 4(x*y) / 2 Simplificamos la parte de la derecha:
(x + y)2 = r2 + 2(x*y) Desarrollamos el paréntesis del primer miembro
x2 + 2xy + y2 = r2 + 2xy Restamos 2xy en los dos miembros
x2 + y2 = r2
Pues ya está hecho... fácil, no? : )
0 comentarios