8ª demostración del Teorema de Pitágoras o demostración de Vieta
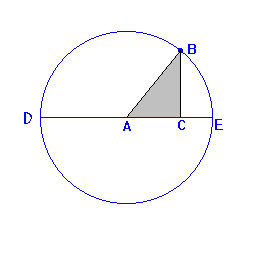
Y vamos ahora con la octava demostración de 367 del archifamoso Teorema de Pitágoras. Para ello, hemos de recordar la definición de potencia de un punto que ya explicamos en la sexta demostración, pero esta vez, el punto fijo está dentro de la circunferencuia y se llama C.
Expresamos las siguientes igualdades:
DC = DA + AC = AB + AC
CE = AE - AC = AB - AC
ya que AE = AB por ser este el radio de la circunferencia.
Usamos la definición de potencia de un punto, que expresamos así:
DC · CE = CB2 (1)
DC · CE = (AB + AC)·(AB - AC)
DC · CE = AB2 - AC2 (2)
Igualamos (1) y (2):
CB2 = AB2 - AC2
AB2 = CB2 + AC2 Quod erat demostrandum (Q.E.D.)
1 comentario
Sadie -
esta es mi demostración favorita!