7ª demostración del Teorema de Pitágoras (de 367) o demostración de Garfield

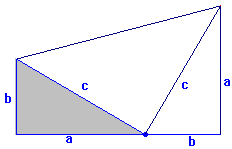
   Basta con calcular el área de la figura de dos formas distintas:

   La figura (completa) es un trapecio de bases a, b y altura a+b, que según la fórmula del área del trapecio [(bas mayor + bas menor) · altura / 2] podemos expresarlo así:

   Área = (a+b)·(a+b)/2 = a²/2 + b²/2 + ab

   Tres triángulos rectángulos:

   Área = ab/2 + ab/2 + c²/2 = ab +c²/2

Igualando estas dos expresiones y simplificando:

     a² /2 + b² /2 = c²/2

  Esto es:

      a² + b² = c²        Quod erat demostrandum (Q.E.D.)