La cuadratura del círculo

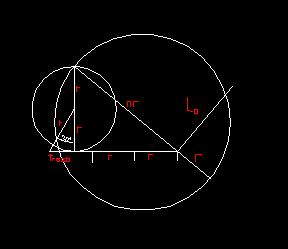
Desde tiempos remotos, los matemáticos intentaron averiguar cómo transformar un cuadrado en un círculo de forma que tengan la misma área. Esto viene dado por la expresión:

         A_cuadrado = A_círculo

          L² = π · r²

Esto de forma aritmética es muy fácil de hallar (le pinchamos a la calculadora y listo) ya que teniendo el radio del círculo puedes calcular su área, luego hallas la raíz de la misma para obtener el lado del cuadrado equivalente. Puede hacerse conociendo el lado del cuadrado y haciendo el mismo proceso a la inversa.

¿Cuál es el problema? Es imposible hallar pi geométricamente. Entonces nos hemos de valer de otro método para trasformar el círculo en cuadrado. La expresión de las áreas puede ponerse de la siguiente manera:

       L² = πr · r

Esta expresión se llama media proporcional (para aquellos que tengan como asignatura el dibujo técnico sabrán lo que es). Como no podemos hallar pi, recurrimos a otra manera más aproximada.

Comienzo explicando el concepto de media proporcional. Si exponemos la relación: un segmento a es a otro desconocido como ese mismo segmento desconocido es a otro b, que se puede expresar de la siguiente manera:

                  a                  x

            ------------  = -----------

                  x                   b

Producto de extremos es igual a producto de medios:

                 x² = a · b

Si nos revisamos los teoremas del cateto y de la hipotenusa ya demostrados en la 2ª demostración del Teorema de Pitágoras (de 367 conocidas) podemos hallar el segmento media proporcional de otros dos. Recordamos las expresiones:

            b² = a · m      c² = a · n

                      h² = m · n

Si conseguimos que m valga πr y n valga r y los colocamos en el mismo segmento una a continuación del otro podremos hallar el segmento media proporcional que será el lado del cuadrado equivalente. Para ello, hallamos el punto medio del segmento total y desde ese punto trazamos una circunferencia que pase por los extremos. Finalmente trazamos una perpendicular al segmento total por el punto en el que se juntan los otras dos segmentos (πr y r) y el segmento resultante comprendido entre el punto de unión de los dos segmentos y el punto de corte con la circunferencia se llama media proporcional que vale en este caso el lado del cuadrado.

Os preguntaréis quizá por qué el lado está como L y no como L². La explicación es sencilla: aunque la relación entre el producto de m y n sea el cuadrado de la altura, no tiene nada que ver con la representación. si nos fijamos bien, podemos dibujar un triángulo rectángulo como el de la 2ª demostración del TP. También os preguntaréis: ¿Por qué rectángulo? ¿No puede ser otro cualquiera? Y yo os digo: NO Y NO. Sólo puede rectángulo dado el concepto de arco capaz.

Y, para los que no lo sepan, el arco capaz es el lugar geométrico (donde el lugar geométrico es el conjunto de puntos que tienen la misma propiedad) de los puntos del plano desde los cuales se contempla a un segmento desde la misma amplitud (ángulo). Ya hablaremos del arco capaz más adelante, pero ahora centrémonos en la demostración.

Ya la única dificultad que queda por resolver es la obtención de pi de forma geométrica. Como podéis ver en el dibujo, hay un triángulo rectángulo cuyos catetos son uno 2r (donde r es el radio de la circunferencia a transformar) y el otro es la diferencia entre 3r y el trozo que he señalado en la figura y la hipotenusa es πr. Hemos de comprobar que pi es realmente pi.

Según el TP (tantas veces demostrado) el cuadrado de esa hipotenusa ha de ser igual a la suma de esos dos catetos, con lo que empezamos la demostración matemática igualando ambas expresiones:

   π²r² = (2r)² + [3r - trozo]²

Donde el trozo es, según la trigonometría:

   Tan  = (cateto opuesto)/(cateto contiguo)

   Tan  = (trozo)/(radio de la circunferencia)

   Trozo = (Tan Â) · (radio de la circunferencia)

Si  vale 30º como se indica en la figura:

   Trozo = [(3)^(1/2)/3] · r

Y seguimos donde lo dejamos:

   π²r² = 4r² + (3r - [(3)^(1/2)/3] · r)²

   π²r² = 4r² + (9r² + (1/3)r² - 2 · (3)^(1/2) · r²)

   π²r² = ( 4 + 9 + (1/3) - 2 · (3)^(1/2) ) · r²

La r al cuadrado se van de paseo cogidos de la mano.

   π² = ( 40 - 6 · (3)^(1/2) )/3

   π = 3.14153333807

   π = 3.14159265358

Como podemos ver, el valor de pi es bastante aproximado al real con una aproximación de más del 99,99%, con lo que podemos dar a este método de transformación como correcto.

Pero aún podemos ir más allá de la cuadratura de círculo. Una pregunta que fue también formulada por muchos matemáticos muchos años atrás, fue la relación entre la longitud de la circunferencia y el radio.

Antes de que se conociese el valor de pi, los matemáticos de antaño recurrieron a un dato algo aproximado siguiendo una demostración que hoy se conoce como la rectificación de un segmento curvo.

Como el potencial del blog no nos da para poner dos imágenes en el encabezado ni para siquiera ver alguna durante todo el escrito, al menos imaginaros lo siguiente:

Dada una circunferencia de diámetro d, dividimos su diámetro en siete partes iguales (con el teorema de Tales o a ojo, como queráis siempre que dado un concepto abstracto se tenga una idea perfecta y más acorde con el mundo inteligible o de las ideas (¡maldito Platón!)). La medida del diámetro la prolongamos dos veces hacia la derecha y, hacia la izquierda, prolongamos la séptima parte del diámetro ya dividido antes.

Si la fórmula de la longitud de la circunferencia es:

   L = k · d 

Donde la k es una constante que pasará a ser pi.

   Postulamos que la longitud de la circunferencia es todo el segmento que hemos dibujado:

   L = (1/7) · d + 3 · d

   L = (22/7)d

Si igualamos:

   (22/7)d = k · d

   k = 22/7

   22/7 = 3.142857142

   pi = 3.14159265358

Con lo que tenemos una aproximación del 99,96% del valor de pi, por tanto, podemos dar este método como válido.

En definitiva, podemos ver que las Matemáticas sirven de apoyo a otras disciplinas o ciencias, como la Física, la Química, La Biología en menor parte, la Estadística, el Dibujo Técnico en este caso entre otras... Según todo esto podemos considerar a las Matemáticas o la Matemática como LA REINA DE LAS CIENCIAS ya que sirve de apoyo o base para todas las demás.

Este artículo no podría haber sido posible sin la enseñanza del catedrático Rafael De Heredia, profesor de Dibujo Técnico.