Teorema de Pitágoras Vs. Número Áureo
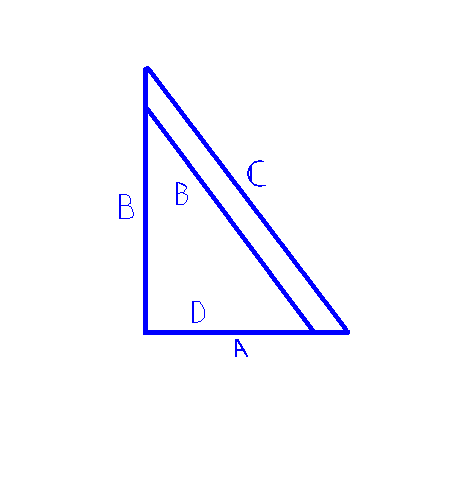
Tomamos dos triángulos rectángulos semejantes los cuales han de compartir el ángulo recto y que las hipotenusas sean paralelas. Los catatos y la hipotenusa del mayor se llaman a, b y c respectivamente y llos del menor a, d y b respectivamente.
Calculamos su razón de semejanza:
a/d = b/a = c/b = r (razón de semejanza)
Por tanto, debe ser:
a = d · r
b = a · r
c = b · r
Y tenemos:
b = a · r = d · r · r = d · r2
c = b · r = d · r2 · r = d · r3
Así tenemos los valores a, b y c en función de d y r. Al ser rectángulos los triángulos, han de verificar el Teorema de Pitágoras (10 veces demostrado aquí).
c2 = a2 + b2
(d · r3)2 = (d · r)2 + (d · r2)2
Ya que d y r son positivos, se puede simplificar dividiéndola por (d · r)2 y quedaría así:
r4 = 1 + r2
Vamos a hallar r resolviéndolo como una ecuación bicuadrada (r2 = t)
t2 - 1 - t = 0
t = (1 ± √5)/2
Los resultados han de ser positivos, por tanto:
t = (1 + √5)/2 = Φ
Por tanto r.....
r = √Φ
Esto nos quiere decir que el Teorema de Pitágoras tiene relación con el número aúreo mediante la expresión ya expuesta.
0 comentarios