3ª demostración del Teorema de Pitágoras

China: el Chou Pei Suan Ching, y el Chui Chang Suang Shu:
El Chou Pei es una obra matemática de datación discutida, aunque se acepta mayoritariamente que fue escrita entre el 500 y el 300 a.C. (Anterior a Pitágoras). Se cree que Pitágoras no conoció esta obra. En cuanto al Chui Chang parece que es posterior, está fechado en torno al año 250 a. C.
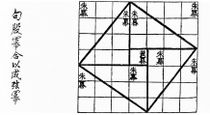
El Chou Pei demuestra el teorema construyendo un cuadrado de lado (a+b) que se parte en cuatro triángulos de base a y altura b, y un cuadrado de lado c (imagen de arriba). Los lados a y b son los catetos y el lado c es la hipotenusa.
Utilizando la nomenclatura de la imagen queremos demostrar que c2 = a2 + b2
Es evidente que el área del cuadrado mayor es igual a 4 veces el área de uno de los triángulos más el área del cuadrado pequeño que queda en el centro. El lado de este cuadrado central es b - a, con lo cual su área es (b - a)2.
Área de un triángulo: (ab)/2
c2 = 4(ab)/2 + (b - a)2 =2ab + b2 + a2 - 2ab = a2 + b2
Q.E.D
0 comentarios