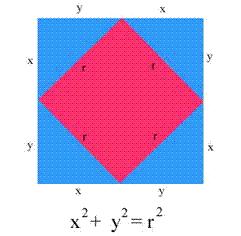
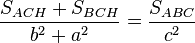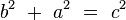El objetivo de Euclides era probar que √2 no se puede escribir como una fracción. Debido a que usó una reducción al absurdo el primer paso es suponer que lo contrario es cierto, es decir, que √2 se podría escribir como alguna fracción desconocida. Esta hipotética fracción se representa p/q, donde p y q son dos números enteros.
antes de embarcarnos en la demostración en sí, todo lo que se requiere es una comprensión básica de algunas propiedades de las fracciones y los números pares.
1) Si se toma cualquier número y se multiplica por 2, el nuevo número será par.
2) Si se sabe que el cuadrado de un número es par, entonces el número mismo debe ser también par.
3) Las fracciones se pueden simplaficar: 16/24 es lo mismo que 8/12; sólo hay que dividir numerador y denominador de la primera fracción por 2 (factor común). Es más, 8/12 es lo mismo que 4/6, que es lo mismo que 2/3. Sin embargo 2/3 no puede ser simplificado porque dos y tres no tienen factores comunes. Es imposible continuar simplificando una fracción por siempre.
Ahora recordemos que Euclides cree que √2 no se puede escribir como una fracción. Sin embargo adopta el método de prueba por contradicción y trabaja con la suposición de que la fracción p/q existe y explora las consecuencias de su existencia:
√2 = p/q
Si se elevan ambos miembros al cuadrado:
2 = p2/q2
Multiplicamos ambos miembros por q2
2q2 = p2
Ahora, según el punto 1, sabemos que p2 debe ser par. Es más, por el punto 2 sabemos que el mismo p también ha de ser par. Pero si p es par entonces se puede escribir como 2m, donde m es otor número entero. esto se sigue del punyo 1. Lo introducimos en la ecuación y resulta:
2q2 = (2m)2 = 4m2
Dividimos por 2 ambos lados:
q2 = 2m2
Pero por el mismo argumento que el usado antes sabemos que q2 debe ser par, y así el mismo q también tiene que ser par. Si éste es el caso, entonces q se puede escribir como 2n, donde n es algún otro número entero. Si volvemos al principio, entonces:
√2 = p/q = 2m/2n
La fracción 2m/2n se puede simplificar dividiendo el numerador y el denominador por 2, y se obtiene:
√2 = m/n
Ahora se obtiene una fracción m/n que es más sencilla que p/q.
Sin embargo nos encontramos en la posición de poder repetir exactamente el mismo proceso sobre m/n, y al final del proceso generamos una fracción aún más sencilla, digamos g/h. Esta fracción puede ser pasada otra vez por la piedra del molino, y la nueva fracción, llamémosla e/f, será más simple aún. Podemos volver a tratar esta fracción y repetir el proceso una y otra vez, en una sucesión sin fin. Pero por el punto 3 sabemos que las fracciones no pueden simplificarse indefinidamente. Siempre existe la fracción más simple, pero nuestra fracción hipotética original p/q no parece obedecer esta regla. Por lo tanto, estamos justificados para decir que hemos encontrado una contradicción. Si √2 se pudiera escribir como una fracción la consecuencia sería un absurdo, y así lo correcto es decir que √2 no se puede escribir como una fracción. Por tanto √2 es un número irracional.
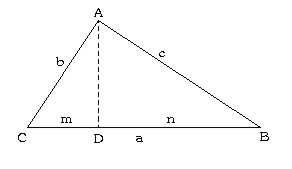
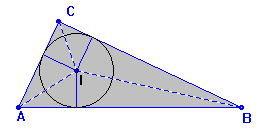
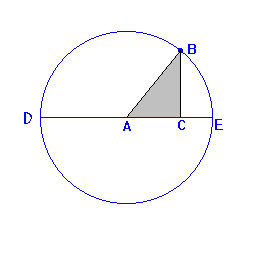
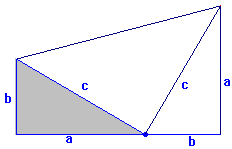
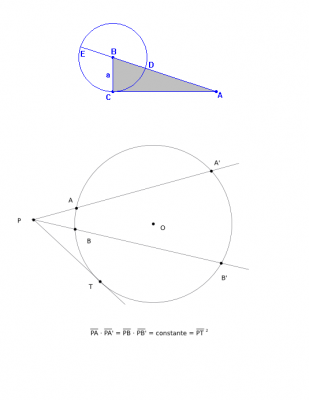
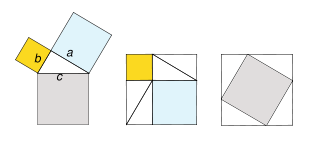

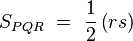
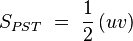
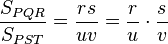
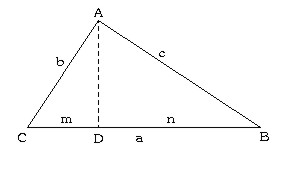
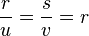 la razón de semejanza, está claro que:
la razón de semejanza, está claro que: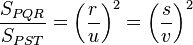

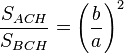
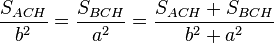 (I)
(I) 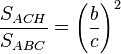
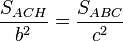
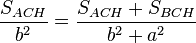 , así que:
, así que: